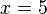Ecuaciones

+

Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes oconstantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:

La letra x representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. Resolver una ecuación es encontrar los valores de las incógnitas que la satisfacen, y se llama soluciónde una ecuación a cualquier valor de dichas variables que cumpla la igualdad planteada. Para el caso dado, la solución es:

Todo problema matemático puede expresarse en forma de una o más ecuaciones. Sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. También puede ocurrir que haya varios o incluso infinitosconjuntos de valores que la satisfagan.

En el caso de que todo valor posible de la incógnita haga cumplir la igualdad, la expresión se llama identidad. Si en lugar de una igualdad se trata de una desigualdad entre dos expresiones matemáticas, se denominará inecuación. Una ecuación funcional es aquella en la que algunas de las constantes y variables que intervienen no son realmente números sino funciones; y si en la ecuación aparece algún operador diferencial se llama ecuación diferencial.
¿Qué es una ecuación cuadrática?

Es un tipo de ecuación particular en la cual la variable o incógnita está elevada al cuadrado, es decir, es de segundo grado. Un ejemplo sería: 2X² - 3X = 9. En este tipo de ecuación no es posible despejar fácilmente la X, por lo tanto se requiere un procedimiento general para hallar las soluciones.

Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica:

,

donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el campo de los números reales o el de los números complejos.

Si tenemos la ecuación general y=ax3 +bx2 + cx + d = 0 mediante el cambio de variable z = x + b/3a; pasamos a otra ecuación, llamada reducida de la forma:

Y=x3 + cx +d =0. Esta ecuación se resuelve mediante las formulas de Cardano, pero nosotros utilizaremos otro enfoque.

En el caso de la ecuación cúbica la relación entre sus coeficientes y raíces, esta dada por:

x1+x2 + x3 = -b; x1x2 + x1x3 + x2x3 = c; x1x2x3 = -d

Para el caso de la ecuación reducida b=0: . x1+x2+x3=0 :. x3 = -(x1 +x2); que reemplazado en la ecuación de c, tendremos x1x2 + x3(x1 +x2 ) = x1x2 -(x1 +x2) 2 =

x1 x2 -(x12 + x22 +2x1x2) =c: . x12 + x22 + x1x2 +c=0.

Ahora expresaremos x2= f(x1)

x2= -x1/2 (x1/2)2 -(c+ x12 ) = -x1/2 -(3/4x12 +c) =- x1/2 i 3(x1/2)2 +c